S tih će se točaka izvršiti na terenu izmjera, a s preslikanih točaka na plohi projekcije izradit će se onda model prostora.
Na teritoriju koji treba izmjeriti izabrat će se najprije relativno mali broj dosta udaljenih točaka, čije će se koordinate prvenstveno odrediti. Te se osnovne točke izabiru tako, da čine suvislu mrežu trokuta ili sustav lanaca trokuta. Da bi se mogle odrediti sferoidne koordinate tih točaka, treba u toj mreži imati najmanje jednu točku poznatu po sferoidnim koordinatama, najmanje jednu dužinu stranice u nekom trokutu i najmanje jedan azimut, tj. kut što ga zatvara stranica s meridijanom kroz jednu od krajnjih točaka te stranice. Ako se u toj mreži izmjere svi kutovi u svim trokutima, bit će koordinate svih ostalih točaka jednoznačno određene.

Mreža trokuta i sistem lanaca trokuta.

Takav postupak određivanja točaka naziva se triangulacijom a tako određene točke nazivaju se trigonometrijske točke ili trigonometri.

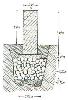
Trigonometar I reda.

Određivanje sferoidnih koordinata početne točke takve trigonometrijske mreže vrši se astronomskim putem, čime se bavi posebna grana astronomije - poziciona astronomija.
Početni azimut jedne trigonometrijske stranice dobiva se posebnim metodama pozicione astronomije, koje se svode na mjerenje kuta između te stranice i određenih nebeskih tijela - zvijezda ili Sunca.
Budući da su stranice trokuta osnovne trigonometrijske mreže duge od 20 do 50 km, dužina početne strane - operacione baze - ne može se mjeriti postojećim pomagalima direktno, nego se do njene dužine dolazi posredno. U tu se svrhu mjeri neka manja dužina - mjerena baza, od koje se posebnim sistemom trokuta, bazisnom mrežom i mjerenjem kutova u njoj prelazi na početnu stranu triangulacije. Ta se strana onda naziva operacionom bazom. Na slici je prikazana shema bazisne mreže.

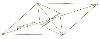
Shema bazisne mreže.

Mjerenu bazu potrebno je izabrati na približno ravnom terenu, obično u dužini od četiri do šest kilometara ili više, ovisno o terenskim prilikama.

Da bi se izbjeglo nagomilavanje pogrešaka, tj. da bi se izbjeglo računanje koordinata točaka koje su relativno daleko od baze preko mnogo trokuta, u triangulaciji se, kao i u svakoj drugoj geodetskoj operaciji, primjenjuje metoda mjerenja iz velikoga u malo. Ta metoda u triangulaciji znači da se preko cijelog izmjerenog teritorija rastegne mreža sa stranama dužine 20 do 50 km, ovisno o terenskim prilikama i više. Zatim se u mreži pogreške izjednače, te se prvenstveno izračunaju koordinate tih točaka. To je trigonometrijska mreža I reda. U tu mrežu umeću se točke II reda s dužinama stranica od 15 do 25 km, pri čemu se koordinate točaka I reda, iz kojih se računaju točke II reda uzimaju kao bespogrešno zadane. Tako se redom u mreže višeg reda umeću točke nižeg reda, pa se trigonometrijska mreža dijeli na:

1. mrežu I reda,
2. osnovnu trigonometrijsku mrežu II reda s dužinama strana od 15 do 25 km,
3. popunjavajuću trigonometrijsku mrežu II reda s dužinama strana od 9 do 18 km,
4. osnovnu trigonometrijsku mrežu III reda s dužinama strana od 5 do 13 km,
5. popunjavajuću trigonometrijsku mrežu III reda s dužinama strana od 3 do 7 km,
6. trigonometrijsku mrežu IV reda s dužinama strana od 1 do 4 km.

Trigonometar II - IV reda.

Srednja gustoća razvijene trigonometrijske mreže svih redova je takva, da prosječno na 200 ha površine dolazi po jedna trigonometrijska točka bilo kojeg reda.

Pojmovi